Теперь Вы можете заказать у нас и решение задач по теормеху!
Наши контакты вверху, пишите!

Специалисты с техническим образованием или попросту будущие инженеры это, прежде всего те люди, которые имеют возможность работать во всех сферах народного хозяйства. Инженер без труда найдет себе работу, ведь существует масса вариантов: работа на заводе, в шахте, работа с транспортом и другое. И все это по тому, что количество инженерных специальностей достаточно велико – мастер, инженер, начальник смены, ведущий инженер и также непосредственно руководитель производственного процесса. Но для того, что бы достичь определенных высот в данной профессии следует хорошо окончить высшее учебное заведение. Студенты, которые учатся на инженерной специальности, непременно будут изучать такую дисциплину, как теоретическая механика. Теоретическая механика – это наука о законах механического движения и взаимодействия материальных тел. Данная дисциплина является одной из базовых в подготовке современных инженеров. Так как теормех является одним из разделов физики, изучать данную дисциплину студенты начинают еще с первого курса. Таким способом, пока их знания в области физики еще не затерялись где то в глубинах сознания, изучение предмета проходит в более живом ритме. И все же не стоит забывать, что для полного понимания данной дисциплины, студент должен обладать глубоким пониманием физики и математики. И если же в одной из этих дисциплин у вас есть пробелы, тогда к вашему вниманию предоставляется онлайн помощь по теормеху.

Теоретическая механика является той учебной дисциплиной, где каждый закон и понятия четко обоснованы, методология ее установлена по определенным дозированным принципам. В свою очередь это означает, что без знания соответствующего теоретического материала и на одной импровизации здесь не выкрутишься. А о последней, даже и речи не может быть. Поэтому все задачи, что будут рассматриваться при изучении теоретической механики, требует от студента предельной точности и глубокого переосмысления теоретических основ данной дисциплины. Заказать срочное решение задач по теормеху возможно буквально в любое время суток. Это будет для вас одним из способов, с помощью которого вы получите хорошую оценку и при этом, проанализировав уже выполненные задания специалистами, вы докопаетесь до сути.

Таким образом, в нашей стране профессии инженера считается одной из распространенных. В этом нет ничего удивительного, ведь логичным есть производство товаров и продуктов широко потребления. А это в свою очередь требует постоянного и всеобщего контроля и управления. С этими задачами могут справиться лишь специалисты соответствующей инженерной специальности. Но очевидным является тот факт, что парни, которым свойственна профессия инженера порой не с таким уж энтузиазмом подходят к учебе. Дабы успеть и отдохнуть, и поучится, у них есть возможность заказать решение задач по теормеху, от которого им некуда не деется как будущим специалистам технической профессии.

Примеры решаемых задач:

ЗАДАЧА № 1

Стержень AB длиной l движется так, что одна из его точек описывает окружность радиусом r<l/2, а сам стержень проходит через неподвижную точку N, лежащую на той же окружности. Составить уравнения движения точки B если j=wt

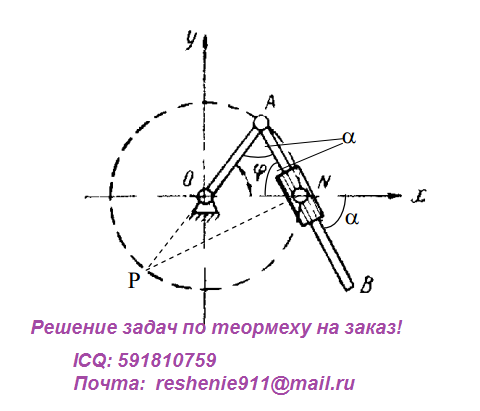
Порядок решения:

Из треугольника OAN находим альфа.

Находим координаты точки В.

Находим закон изменения координат для точки B.

ЗАДАЧА № 2

Гибкая нерастяжимая нить АВСD одним концом закреплена в точке D, а другим перекинута через неподвижный блок B находящийся на той же высоте что и точка D причем расстояние BD=a. В точке С нити закреплен груз М, DC=b. Определить модуль вертикальной составляющей скорости груза М в зависимости от угла j, образованного частью нити CD с вертикалью, если конец А нити тонут с постоянной скоростью u.

ЗАДАЧА № 3

Точка движется в пространстве с постоянным ускорением `w направленным параллельно оси Ох и равным по модулю 5 м/с². В начальный момент точка имела скорость `v₀ равную по модулю 5м/с и образующую с осями Ох и Оу соответственно углы a=60° в и b=45°. Определить радиус кривизны траектории точки в момент времени t=1с.